
PRINCIPIO DE ARQUÍMEDES
El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.
La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:
-
El estudio de las fuerzas sobre una porción de fluido en equilibrio con el resto del fluido.
-
La sustitución de dicha porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Porción de fluido en equilibrio con el resto del fluido.
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, dondep solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=rf·gV

El peso de la porción de fluido es igual al producto de la densidad del fluido rf por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.
Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto.
En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje.
La presión debida al fluido sobre la base superior es p1= ρfgx, y la presión debida al fluido en la base inferior es p2= ρfg(x+h). La presión sobre la superficie lateral es variable y depende de la altura, está comprendida entre p1 y p2.

Las fuerzas debidas a la presión del fluido sobre la superficie lateral se anulan. Las otras fuerzas sobre el cuerpo son las siguientes:
· Peso del cuerpo, mg
· Fuerza debida a la presión sobre la base superior, p1·A
· Fuerza debida a la presión sobre la base inferior, p2·A
En el equilibrio tendremos que
mg+p1·A= p2·A
mg+ρfgx·A= ρfg(x+h)·A
o bien,
mg=ρfh·Ag
Como la presión en la cara inferior del cuerpo p2 es mayor que la presión en la cara superior p1, la diferencia es ρfgh. El resultado es una fuerza hacia arriba ρfgh·A sobre el cuerpo debida al fluido que le rodea.
Como vemos, la fuerza de empuje tiene su origen en la diferencia de presión entre la parte superior y la parte inferior del cuerpo sumergido en el fluido.
Con esta explicación surge un problema interesante y debatido. Supongamos que un cuerpo de base plana (cilíndrico o en forma de paralepípedo) cuya densidad es mayor que la del fluido, descansa en el fondo del recipiente.

PRINCIPIO DE PASCAL
En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: la presiónejercida en cualquier lugar de un fluido encerrado e incompresible se transmite por igual en todas las direcciones en todo el fluido, es decir, la presión en todo el fluido es constante.
La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.
También podemos ver aplicaciones del principio de Pascal en las prensas hidraulicas.
PRENSA HIDRAULICA
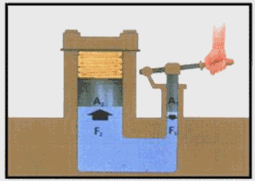
La prensa hidráulica es una máquina compleja semejante a un camión de Arquímides, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección S1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma (casi) instantánea a todo el resto del líquido. Por el principio de Pascal esta presión será igual a la presión p2 que ejerce el fluido en la sección S2, es decir:
p_1 = p_2 ,
con lo que, las fuerzas fueron siendo, siendo S1 < S2 :
F_1 = p_1 S_1 < p_1 S_2 = p_2 S_2 = F_2,
y por tanto, la relación entre las fuerza resultante en el émbolo grande cuando se aplica una fuerza menor en el émbolo pequeño será tanto mayor cuanto mayor sea la relación entre las secciones:
TEOREMA DE BERNOULLI
El teorema que por primera vez enunció Daniel Bernoulli en el año 1726, dice: en toda corriente de agua o de aire la presión es grande cuando la velocidad es pequeña y, al contrario, la presión es pequeña cuando la velocidad es grande.
La dinámica de los líquidos, está regida por el mismo principio de la conservación de la energía, el cual fue aplicado a ellos por el físico suizo Daniel Bernoulli (1700-1782), obteniendo como resultado una ecuación muy útil en este estudio, que se conoce con su nombre.
El teorema que por primera vez enunció Daniel Bernoulli en el año 1726, dice: en toda corriente de agua o de aire la presión es grande cuando la velocidad es pequeña y, al contrario, la presión es pequeña cuando la velocidad es grande. Existen algunas limitaciones a este teorema, pero aquí no nos detendremos en ellas.Teorema de Bernoulli y sus Consecuencias
Por el tubo AB se hace pasar aire. Donde la sección de este tubo es pequeña (como ocurre en a), la velocidad del aire es grande, y donde la sección del tubo es grande (como en b), la velocidad del aire es pequeña. Si la velocidad es grande, la presión es pequeña, y donde la velocidad es pequeña, la presión es grande. Como la presión del aire en a es pequeña, el líquido se eleva por el tubo C; al mismo tiempo, la gran presión del aire en el punto b hace que el líquido descienda en el tubo D .
Para ello se puede considerar los puntos 1 y 2, de un fluido en movimiento, determinando la energía mecánica de una porción de éste, a lo largo del filete de fluido en movimiento que los une.
Si m es la porción de masa considerada υ, su rapidez, Υ la altura sobre el nivel tomado como base, la presión y a densidad en cada uno de los puntos, se puede escribir utilizando el teorema trabajo-energía cinética:

Si ahora se di vide a todos los términos de los dos miembros, entre la masa considerada, se obtendrá la ecuación de Bernoulli, que corresponde a la ley de la conservación de la energía por unidad de masa. Si el fluido es incompresible, como supondremos en lo sucesivo, donde (P1 = P2 = P), la ecuación de Bernoulli adopta la forma:
Así como la estática de una partícula es un caso particular de la dinámica de la partícula, igualmente la estática de los fluidos es un caso especial de la dinámica de fluidos. Por lo tanto, la ecuación (6.10) debe contener a la ecuación (6.5) para la ley de la variación de presión con la altura para un fluido en reposo. En efecto, considerando un fluido en reposo, y reemplazando (υ1 = υ2 = υ) en la ecuación de Bernoulli, se obtiene:
que es precisamente la ecuación fundamental de la estática de fluidos.
Ejemplo
Fluido humano. Una multitud de espectadores pretende salir de una gran sala de proyecciones al término de la función de cine. El salón es muy ancho, pero tiene abierta al fondo sólo una pequeña puerta que franquea el paso a una galería estrecha que conduce hasta la calle. La gente, impaciente dentro de la sala, se aglomera contra la puerta, abriéndose paso a empujones y codazos. La velocidad con que avanza este “fluido humano” antes de cruzar la puerta es pequeña y la presión es grande. Cuando las personas acceden a la galería, el tránsito se hace más rápido y la presión se alivia. Si bien este fluido no es ideal, puesto que es compresible y viscoso (incluso podría ser turbulento), constituye un buen modelo de circulación dentro de un tubo que se estrecha. Observamos que en la zona angosta la velocidad de la corriente es mayor y la presión es menor.

